勉強へのモチベーションってなかなか続かない時があります。どうしたらよりモチベーションを保つことができるのでしょうか？今回は、「40日で一兆歩理論」という新しい行動へのやる気を刺激してくれる理論を紹介します。これを読むと「継続の大切さ」がよくわかる、かもしれません。

先日「選択の自由メソッド」の記事で、１日１回二者択一の選択を365日続けたら、どうなるか？という話しをしました。

こういう累乗の力を表す話しは、よく金利の複利計算の話しなどでよく出てくる例えです。
似たような話しで「紙を何回折ったらどのくらいの厚さになるのか？」という話しがあります。「紙を40回ほど折ると、なんと月まで届くほどの厚さになる」というお話です。実際には６回〜７回でそれ以上は折れないほどの厚さになってしまうのですが、もしそれ以上折り続けることができたら、計算上そうなる、という話しです。

有名な話しですので、聞いたことがあるかもしれません。

こういうのを聞くとたしかに「すごいな」と思います。でも、実際には40回も紙を折れないわけだし、現実に役立つこともないので、私もこの話しを聞いて、感心して終わっていました。

ところが、「選択の自由メソッド」の記事を記事を書いていて、気付いたんです。この累乗の話しって、よく考えると、かなりすごいことかもしれない、ということに。そしてこの考え方は、現実の世界でやる気を起こすのにすごく役に立つかもしれない、ということに・・・。

「選択の自由メソッド」は、「無量大数」を超えてしまう話しで、ちょっと桁が大きくなりすぎてわかりにくいので、もう少し数を小さくして考えてみましょう。

2×2×2×2・・・を40回繰り返すと１兆を超える、というのが「紙とお月様の話し」です。

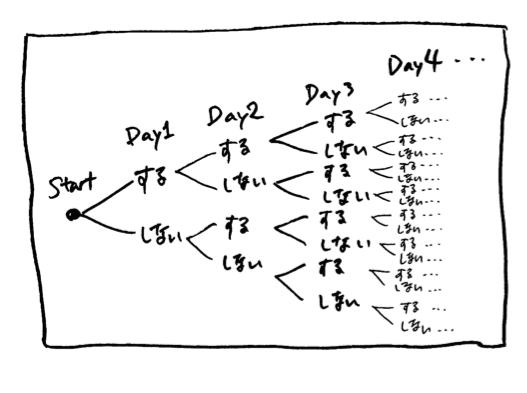
・・・と言うことは１日１回「英語の勉強をする」「英語の勉強をしない」という２つの選択肢からどちらかを選ぶ、ということをすると、40日後にはなんと１兆通りもの組み合わせのパターンができる、ということです。

このイラストの「Day4」のところの可能性は16通りですが、ずっと右へ行って「Day40」のところには１兆通りもの可能性があるのです。40日間何もしなかった場合（つまり図の「Day40」の一番下の場合）と比べて、40日間毎日英語の勉強を少しでもした場合（つまり図の「Day40」の一番上の場合）「一兆歩」もの違いがある、ということになる、ということだと思うのです。

自分でも数が大きくなりすぎてよく訳が分からなくなってきたので、数学とか確率とか得意な方、理論的におかしなところがあったら教えてください。（問い合わせフォームからお願いします）

もしこの理屈が正しいとすると、40日の間毎日一歩一歩休まずに歩みを進めていくと、40日後には「40歩進む」のではなく「一兆歩進む」ことができているのではないか、と思うのです。

「継続は力なり」ということわざがあります。このことわざの真意は実はこういうことなのでしょうか？

そういえば、グーグルの検索エンジン関係の偉い方のマット・カッツという方の『30日間チャレンジ』というTEDスピーチがあります。

これは、どんなことでも30日間続けると結構いろんなことができるようになってしまいますよ、という話しですが、これも結局この「40日で一兆歩理論」なのかもしれません。

40日後一兆歩前に進めると思ったら、毎日少しでも勉強しよう！って思いません？1mmを40回折り重ね続けたら、月まで行けるんです。モチベーション上がってきますよね？

私も自分で書いていてモチベーションが上がってきました。今までやろうと思って先延ばししてきたことを今から始めようと思います。40日後「一兆歩」進んでいるか、試してみます。

追伸：あなたの「月」はどこですか？